SOLD OUT
Quadratic Curve 二次曲線説明器 urushi_Kuro(受注生産品)
二次曲線説明器は、円錐曲線を表現した模型です。
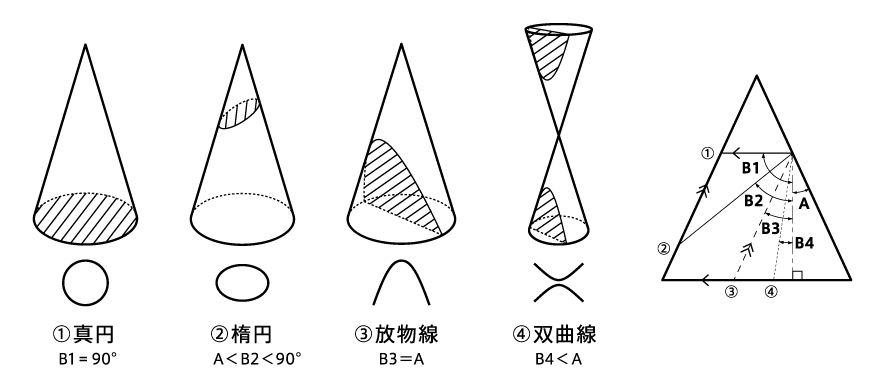
円錐曲線とは円錐を平面で切ったときに切り口に現れる楕円(ellipse)放物線(parabola)双曲線(hyperbola)の3種類の曲線のことです。
Quadratic Curve Urushi_Kuro には、独自に「はな塗」という技法を開発し、古くからそれを使ってきた会津漆器とコラボした製品です。手塗故に漆独特の柔らかい塗膜が美しく際立っています。ひとつのピース毎に漆の艶感を変え、色だけでなく触感も丁寧に仕上げました。ダークトーンの部屋にもブライトトーンの部屋にも馴染む色を配色しています。
こちらはトップピースを蒔絵という技法で本物の金粉を蒔いたものを浮き立たせるためにその他のピースはダークな透き漆で統一しています。(艶感は異なるピースがあります)
受注生産品となっています。納期はお問い合わせください。
110,000円(税込)

暮らしの中に隠れている数学の美しさに光をあて
心を豊かにするモノたちのブランチです
加藤数物製作所で製造していた数理模型たちを
現代的にアレンジしたフラッグシップ商品群です
円錐曲線は、古代ギリシャ時代に発見、考え出されたもので、数々の研究により円錐表面と平面との関係よりいろいろな性質が明らかにされました。
17世紀ころには、さまざまな科学者によって宇宙の動きと関係していることがわかってきました。 ケプラーは太陽系の惑星が太陽を焦点の一つとする楕円軌道を回っていることを、ガリレオは物を投げたときに描く曲線がこの放物線であることを明らかにしました。さらにニュートンは万有引力の法則などニュートン力学をまとめることで、天体の運動も物を投げるときの運動も円錐曲線があてはめられることを証明し、その後パスカルやデカルトによって数学的な表現がなされ、二次曲線としての研究が進みました。
このシンプルな円錐で表現される曲線が、私達のいる地球が今の瞬間も進んでいる軌道であったり、ボールが飛んでいる軌跡であったり、自分たちの身近に接していた曲線であることは、知的な喜びを与えてくれます。
このシンプルな円錐で表現される曲線が、私達のいる地球が今の瞬間も進んでいる軌道であったり、ボールが飛んでいる軌跡であったり、自分たちの身近に接していた曲線であることは、知的な喜びを与えてくれます。